opfcaster.blogg.se - Python gauss seidel methos

We will solve the following system of linear equations:īefore we see the algorithm encoded in Python, we will proceed manually with the Gauss elimination method. Without getting lost in the complications of notation for the general case, we will proceed with an example. The elimination phase proceeds by repeatedly performing the 3rd fundamental operation of the list previously discussed. The first phase has the purpose, as indicated in the previous table, to transform the equations from the form Ax=b to that of immediate solution Ux=c.

It consists of two phases: the elimination phase and the backward substitution phase. It is the most familiar method for solving systems of linear equations. The reason why direct methods of resolution try to transform matrix A into a triangular matrix is immediately evident when writing, for example, Ux=c, which means solving the following system of linear equations:Īs you can see it is easy to solve starting from the last equation. In the table, in the column of the final form of the equations, 3 standard matrices appear, which are: The following table summarizes the 3 main direct methods of resolution: Method Of course these operations do not affect the solutions of the system that remain the same, but they can affect the coefficients of A and its determinant.

Replace a row of A with the one obtained by adding that row with another row multiplied by a scalar (leaves the determinant of A unchanged).

Multiply a row of A by a non-zero scalar λ (the determinant of A is multiplied by the same scalar).

Exchange two lines of A (the determinant of A changes sign).

This transformation can be obtained by applying 3 fundamental operations: Their common feature is that they try to transform the original equations into an equivalent system that is easier to solve. In addition to iterative methods, which we will not talk about here, there are so-called direct methods. Methods of solving systems of linear equations That is, if we modify the input, the system of linear equations to be solved will have a different vector b but the same matrix of coefficients A. The matrix of coefficients A, reflecting the intrinsic characteristics of the system, is independent of the input.

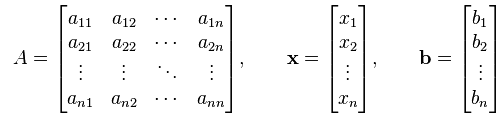
Modeling linear systems gives rise to linear equations of the form Ax = b, where b is the input vector and the vector x represents the response of the system. The broad class of linear systems includes structures, elastic solids, heat flows, electromagnetic fields, electrical circuits and much more. But their most natural application in engineering is in the analysis of linear systems. Linear and algebraic equations can be found in almost all branches of numerical analysis.